Over the past couple months, I’ve been doing something that I never really did much before. While I still think of it as slow and monotonous, and much less efficient than biking and other modes of travel, I’ve decided to turn a new leaf and start running.

There are several reasons for my decision to take up an activity that in the past has only hurt my knees and given me cramps. Soon after arriving in Hungary, I discovered that running is the only practical and cheap alternative for staying fit in Budapest. A number of people in my study abroad program considered gym memberships at the beginning of the year, but I balked at the idea of paying a monthly fee for a gym that was far away and less equipped than Whitman’s free gym (on second thought, should I say “free” gym?).

So I decided against signing up for a membership. Then, as I was looking for something else to do, I discovered that Budapest is an excellent place for running! Once you get off the exhaust-filled streets, there are trails along the Danube, paths crisscrossing City Park, and even a rubberized track around the perimeter of Margaret Island near the city center. Soon after discovering these places, I began a regular running regimen. And now that I’ve joined a group of people in the reckless decision to sign up for a half marathon (coming up this Sunday, April 15—wish me luck!) I certainly can’t stop.

At the Opera House and on Margaret Island. 

If any of you come to Budapest, I would be happy to take you on a running tour of the city. But for those of you who won’t make it before May, here are some photos, a few of my favorite routes in the city (and in other European cities I’ve visited), and a few of the things that I’ve learned while running:

The Classic

My classic run is along the major thoroughfares (also known as ring-roads, in Hungarian korüt) to the Danube. From there I run north along the river to Margaret Island, go once around, and come back by another route. My favorite part is definitely the island, which is less developed and features a rubberized track.

 

City Park

This large tract of land east of city center is not so much of a park as it is a city in itself. City Park contains lakes, trails, restaurants, exercise equipment, public buildings, monuments, museums, the largest thermal bath in the city, and the Budapest zoo, as well as an entire castle. It can be hard to find a long stretch of dirt path, but crisscrossing the paved roads of the park is an excellent way to get in some solid mileage.

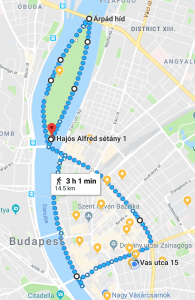
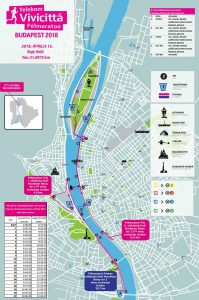
The Half Marathon – River Running

The route for this run has changed from previous years. Instead of passing by the famous landmarks of Budapest in the inner city, most of the run will follow the river (excellent views, but less thrilling overall). We will start and end on Margaret Island, and follow the river down further south than I have been on foot, so I’m excited!

Other Cities: Berlin, Prague, and Vienna, Oh My!

In other European cities, I recommend locating the nearest palace, castle, or imperial gardens, and running there. Usually, one of those three will be within three miles (#europe). I’ve had a lot of fun exploring places as varied as the gardens of Schoenbrunn Palace and the train yards of Prague.

I also would recommend running along whichever river runs through the city, sometime earlier in the day. There will be fewer tourists, better trails, and some excellent views. Just be careful of the swans in Prague. They are large and terrifying if provoked.

 

The swans from afar. DO NOT APPROACH.

At the end of the day…

After spending a good amount of time running, I’ve decided that it is not the worst activity ever. My knees hurt less now than they used to, and I can keep up a good pace over several miles. This past weekend when a group of students from BSM and AIT (a computer science program based in Budapest) met in City Park to play Ultimate, I noticed a significant change since the beginning of the semester. I could keep running as long as I wanted. My legs were fine, and my lungs were fine, and it felt great to push myself the whole time. I still have a long way to come in terms of my Ultimate skill—but one thing at a time, right?

I wish that everything in life were as simple as training for a long run. I know that if I set a proper schedule of long and short routes, punctuating my training with occasional fast runs, then I should gradually notice my stamina and strength improve. At any point in my regimen, I understand what I need to do next.

My experience studying abroad, however, has made it clear that not much works this way. In math and life, I try to plan ahead and work diligently, but I’ve come to realize that I cannot expect the same linear improvement I’ve noticed with my running. There are pitfalls and detours, and more often than not my mathematical proofs and personal projects progress in cycles rather than in efficient trajectories. And there’s never a finish line.

I think that right now, running is just the thing I need. During this week full of political uncertainty in Hungary and this semester of challenging coursework, I appreciate knowing that this Sunday—if I just continue to put one foot in front of the other—everything will turn out just fine.

It’s decided. I had wanted to write this blog post yesterday so that there would be some uncertainty in the outcome in the Hungarian national election, but unfortunately, it’s all too clear: Victor Orbán is still in power. And Hungary may have taken another step away from democracy.

Let me backtrack. Yesterday, April 8, was the Hungarian national parliamentary election. Starting in the early morning, Hungarian citizens in Hungary’s 106 electoral districts cast their votes for one of about ten parties. It was an exciting day, with people lining up for blocks at polling stations and news updates throughout the evening. The U.S. embassy even sent out warnings to avoid Kossuth Square in front of the Parliament Building last night because tensions between the supporters of various parties might be “high.”

The undisputed winner of the election was the Fidesz (fee-DES) party, a nationalist, right-wing organization whose leader, Victor Orbán, has been prime minister for ten years. I find Fidsez frightening for several reasons. First, the party is anti-migration, going to the extreme of building a razor-wire fence along its southern border in 2015 to keep refugees out of the country. Preventing immigrants from entering Hungary is a hallmark of the Fidesz political platform. In addition to enacting xenophobic policies, Orbán’s party has systematically taken control of news media and redrawn electoral districts to keep itself in power. In recent years, the group has moved even more aggressively to alter the Constitution of Hungary in order to control courts, allow for rampant corruption, and according to some critics, effectively dismantle Hungarian democracy.

I am worried for Hungary because I believe that Fidesz poses a real threat. As Princeton University professor Jan-Werner Müller predicted in a recent New York Times Od-Ed piece: “This election is probably the last before Hungary shifts from what is already a deeply damaged democracy to what political scientists would call a full-blown electoral autocracy.”

I can only imagine it’s a scary time for liberals in Hungary. The only Hungarians I interact with regularly—my professors—are relatively reserved about politics, but it’s clear that most of them fall on the left of the political spectrum. From what they’ve said to us, I can sense that progressive Hungarians are frustrated, angry, and tired. We Americans have had Trump for over a year. They’ve had to fight against Orbán for nearly ten years. And the clock just restarted.

The maps of the electoral districts show how much of a landslide victory this was. And in case you’re wondering, the largest opposition party, Jobbik (in black), is even more extreme right than Fidesz. 

One of the critical pieces of information about this election is that turnout was very high. I haven’t found a percentage yet, but as of 3pm yesterday, 54% of Hungary’s voters had already cast a ballot. Government officials have celebrated the turnout as a triumph of democracy. Before yesterday, opposition leaders anticipated that high turnout would disadvantage Fidesz. In fact, the opposite proved true. Fidesz is projected to have another supermajority of 133 of the 199 seats in Parliament. In effect, Fidesz will be able to unilaterally change the Constitution (they received the same number of seats in 2014). This is the mandate that the people have given them, supposedly.

If Orbán is so bad for democracy, I’ve wondered to myself, what happened? How could he and his party have won this election? Gerrymandering certainly played a part in the landslide victory, as well as divided opposition parties. Most of the districts in Budapest could have been won by opposition parties, according to one commentator, if they had not split the vote between them.

However, it can’t be avoided that most Hungarian votes want Fidesz in power. Polling shows that the party and their platform is popular. The majority of Hungarians want to build walls rather than bridges, and they appear to be willing to sacrifice freedoms to achieve the economic and physical security that Fidesz promises.

It’s hard for me to understand, but I’m trying.

More to come on this soon.

Good news! I think that my midterms were successful, so I’ll probably be keeping all of the courses in my schedule. Here’s the rundown:

• Combinatorics 1 (Dezső MIKLÓS)
• Mathematical Problem Solving (Sándor DOBOS)
• Introduction to Topology (Ágnes SZILÁRD)
• Introduction to Mathematical Cryptography (Péter MAGA)
• Intermediate Hungarian

I know most of you are thinking, They offer topology? I wish I could take that! or Combinatorics?! what a lucky duck he is! or I want one of these awesome Hungarian last names!

These are all things that I’m excited about too. And while you probably know all that you need to know about asymmetric cryptographic systems already, I thought that you might appreciate a short review of what my classes entail. Below are some descriptions, as well as some sample problems from the first couple weeks of each course:

Combinatorics 1

The goal of this class is to explore the various ways to count possibilities. We talk a lot about putting hats on people, buying candy and ice cream, and placing people on committees. One of the reasons I like this class is because there are several ways to approach every problem. Depending on how you choose to group objects, you can come up with very different formulas, which I find exciting.

Our professor happens to be the director of BSM, Dezső Miklós, who strides into class five minutes late every day and immediately begins writing on the chalkboard without consulting notes. This is very common for our Hungarian professors, I’ve come to realize. I guess the math is just so ingrained in their psyche, they can pull a lesson plan out of their heads.

Combo Problems

1) How many ways are there to place 1×2 dominoes to exactly cover a 2×10 rectangle?

2) The 5 players of the Chicago Bull are all of distinct heights. In how many different ways can they enter the court if no player is placed between two others both higher then him? Generalize for n players!

Mathematical Problem Solving

This is one of a few courses that make BSM unique from any other undergraduate math program. In this class we explore strategies we can use to solve problems across mathematics. Each week we tackle a different field. One week we looked at divisibility, another week we solved geometry problems, now we are considering problems that involve perfect squares (like 1 = 1², 4 = 2², 9 = 3², or 16 = 4²).

My professor, Sándor Dobos, is also one of the coaches of the Hungarian Math Olympiad team, a group of high school students that competes every year in the International Math Olympiad competition against over a hundred other countries. You can tell that he is loves every field of math. He gets so animated over each proof and reveals the solution to every problem as if it were the end of a murder mystery. He also plays his ocarina (clay flute) to announce the beginning of every problem.

 

 

MPS Problems

3) Prove that every positive integer has a multiple in the form 11…1100…0 (some 1’s followed by some 0’s)

4) Let A and B be points and m be a line. How do you find the point P on m such that AP + PB is a minimum.

Introduction to Topology

  

Topology, says Professor Szilárd (see-LARD), is “seriously exciting.” On our first day of class, she described topology as “rubbersheet geometry.” Unlike in the field of geometry, in topology any two shapes are equal if they can be deformed into another by twisting, compressing, or stretching, as if they were made of rubber. So, all triangles are topologically equivalent, as are squares and circles, spheres and cubes, and all sorts of lines. However, the torus, with its hole, is not equivalent to a sphere.

We calculate that two objects are topologically the same by finding special functions called homeomorphisms that map one objects onto the other. This semester, we’ve used homeomorphisms to show that the sphere minus a point is essentially a plane, and that gluing two one-sided Mobius strips together produces a cool object called a Klein bottle, among other equivalences. Topology is one of the foundational fields in mathematics, so I’m glad to finally be receiving an introduction.

It’s hard to find an introductory problem that doesn’t involve a number of definitions, so maybe this will provide a taste of the terminology:

5) In class we showed some cases of the fact that in R all open intervals (a, b) (where a, b can be ±∞ as well) are homeomorphic. Now consider [0, 1) and (0, 1) of R. We certainly know they are bijective as both are uncountable. Find an actual bijection between the intervals [0, 1) and (0, 1) of R.

Introduction to Mathematical Cryptography

This is probably the sexiest course title in my schedule. Cryptography sounds mysterious and complicated, but it is simply the study of how to send private messages. How can we ensure that a message can get from Alice to Bob without Eve, the eavesdropper, figuring out what the message is? In ancient times, the rudimentary Caesar cipher or simple substitution cipher were sufficient to encode and decode messages secretly. But with the advent of computers, cryptographers have turned to rigorous mathematical algorithms to create cryptographic systems that can securely transmit large amounts of data.

The class has drawn upon other fields I have studied, such as discrete math and abstract algebra, which I thought would never be all that practical. Just goes to show there is almost always an application of math!

Cryptography Problem

6) Crack the following Caesar cipher: iai! oazsdmfgmfuaze! zmftmzuqx iagxp nq ea bdagp ftmf kag eaxhqp ftue oubtqd.

Intermediate Hungarian

Slowly, but surely, I am learning Hungarian vocabulary. For whatever reason, my Spanish keeps coming to me instead of Hungarian. Oh well, maybe I can try Spanish at the local store.

I promise to post again soon!

Nathaniel